Vorbemerkungen
Zum Lesen wähle bitte oben aus der Kapitelauswahl ein Thema aus.
Bitte lies auch die folgenden kurzen Anmerkungen:
- Der Beitrag hat einen bewusst niedrigen Einstiegslevel, um möglichst allen Zugang zum Thema zu geben.
- Das Dezimaltrennzeichen ist in den Abbildungen der Punkt, während es im übrigen Text das in Deutschland gebräuchliche Komma ist.
- Bei Rechenwerten und -ergebnissen verzichte ich bisweilen auf hohe Genauigkeit, also vielen Nachkommastellen.
- Bei Bezeichnern verwende ich, wenn möglich, die aus MS Excel bekannten.
- Klicke oben auf "Deklarationen", um schnell nachschlagen zu können, was was bedeutet.
Prozentrechnung
Manchmal ist es hilfreich, sich die Bedeutung von Worten besonders bewusst zu machen. Prozent bedeutet "für Hundert" (Lateinisch pro = für, centum = Hundert). Will man also wissen, wieviel zum Beispiel 5 Prozent (nachstehend wird nur noch das Prozentzeichen "%" verwendet) von 1.000 sind, so muss man für jede Hundert, die in 1.000 enthalten sind, 5 summieren, also 5 für jede Hundert. So ermittelt man zunächst wie oft die 100 in 1.000 enthalten ist und multipliziert dann das Ergebnis mit 5.

Für den weiteren Verlauf dieses Beitrags favorisiere ich eine andere und - wie ich finde - einfachere Schreibweise für die Prozentrechnung. Wenn man zunächst 5 durch Hundert teilt und die daraus resultierende Dezimalschreibweise nutzt, lassen sich alle einfachen Prozentrechnungen abkürzen.
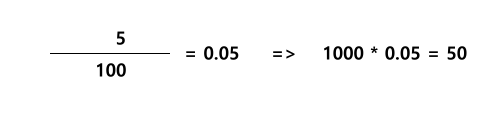
So ist es dann recht einfach beispielsweise 7% von 200 oder 12% von 12.457 zu berechnen:

Wie gesagt, im weiteren werde ich diese Schreibweise in bevorzugen, wenn es um einfache Brüche geht.
Einfache Verzinsung
Vorüberlegung
Leasinggesellschaften bedienen sich u.a. bei der Berechnung von Leasingraten oder dem Wert von vertraglich entstandenen zukünftigen
Leasingforderungen (also Leasingraten, zu deren Zahlung der Leasingnehmer per Leasingvertrag verpflichtet ist) der Zinsrechnung.
Die Gründe hierfür sind sicherlich interessant und vielfältig, sollen aber im Rahmen dieses Beitrags nicht diskutiert werden.
Wesentlich an dieser Stelle ist jedoch, dass die Zinsrechnung den mathematischen Kern von Berechnungen zu einzelnen oder mehreren
Leasingengagements darstellt.
So könnte zum Beispiel die Vorgabe bei der Erstellung eines Leasingangebots sein, dass man beim Einsatz von 100.000 €, die man
für den Kauf eines Leasingobjektes benötigt (z. B. ein Baukran), durch die vom Leasingnehmer zu zahlenden Leasingraten eine Verzinsung
von insgesamt 8% pro Jahr erzielen möchte. Diese 8% decken zum einen die Finanzierungskosten der Leasinggesellschaft zum anderen auch
Kostenanteile für Gehälter, Büromieten, Telefonentgelte etc. Wie die Leasinggesellschaft zur Bestimmung des jeweiligen Zinssatzes kommt,
soll hier auch nicht weiter erörtert werden.
Die Frage, die hier geklärt werden soll, ist: Wie wird die Vorgabe, z. B. 8% pro Jahr erzielen zu wollen, mathematisch umgesetzt?
Gegenwartswert und Zukunftwert
Ein Beispiel:
Du zahlst 1.500 € auf ein Sparbuch zum 1. Januar eines Jahres ein. Die Bank verspricht Dir 2% Zinsen pro Jahr, die zum Jahresultimo (letzter Tag des Jahres) ausgezahlt werden. Wieviel EURO Zinsen zahlt Dir die Bank zum Jahresende?
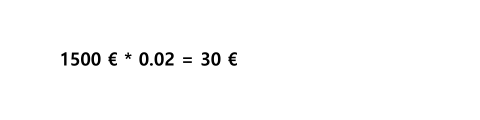
Zum Jahresende hast Du also die zuvor eingezahlten 1.500 € (1.500 * 1) zuzüglich der 30 € (1.500 * 0,02) Zinsen auf dem Sparbuch. Vereinfacht zuammengefasst also:

Also im Ergbnis 1.530 €.
Nun ist eine gute Gelegenheit zwei Begriffe einzuführen. Die am 1. Januar gezahlten 1.500 € stellen den sog. Gegenwartswert oder auch Barwert des Einzahlungsbetrags dar. Der am 31. Dezember entstandene Gesamtbetrag von 1.530 € ist der Zukunftswert oder auch Endwert des eingesetzten Geldes.
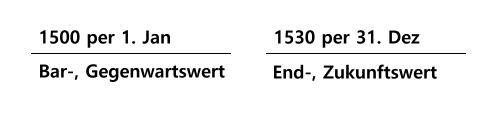
Aufzinsungsfaktor und Abzinsungsfaktor
Wir haben gesehen, dass wir den Endwert des eingezahlten Geldbetrages durch Multiplikation mit dem Faktor 1,02 errechnet haben. Dieser Faktor 1,02 nennt sich Aufzinsungsfaktor.
Will man aus einem bekannten Endwert (Zukunftswert) den Barwert (Gegenwartswert) errechnen, so muss man den Rechenvorgang umkehren, indem man den Endwert durch den Aufzinsungsfaktor teilt.
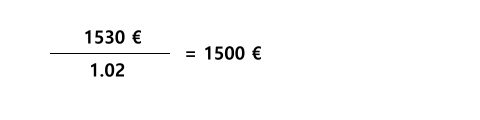
Anders geschrieben sieht das folgendermaßen aus
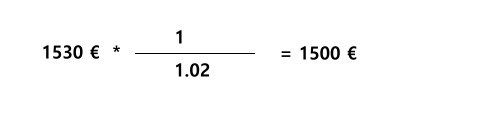
Wandelt man den Bruch in eine Dezimalzahl um so erhalten wir
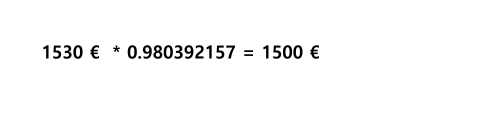
Der Faktor 0,980392157 stellt den sogenannten Abzinsungsfaktor dar. Er ist der inverse Wert (Umkehrwert) des Aufzinsungsfaktors und wurde ermittelt, indem wir 1 durch den Aufzinsungsfaktor geteilt haben.
Der guten Ordnung halber sei noch auf folgendes verwiesen:
Es kann ja auch sein, dass man sein Geld unterjährig (beispielsweise am 14. Juni) einzahlt, was eine andere Vorgehensweise bei der
Berechnung der Zinsentwicklung erfordert. Unterstellt man weiterhin, dass die Bank jeweils zum Ende des Kalenderjahres Zinsen gutschreibt,
dann müsste man tagesgenau zunächst sein Guthaben per Ende des laufenden Jahres errechnen, also den Kontostand, nachdem die Bank die Zinsen
zum Jahresultimo gutgeschrieben hat. Wenn der Betrachtungszeitraum 1 Jahr ist, wird der Kontostand zum 14. Juni des Folgejahres sich im
Vergleich zum Endstand per Ende des ersten Kalenderjahres nicht verändert haben, da die Bank die Zinsen ja erst zum Ende des Folgejahres
gutschreibt. Will man trotzdem wissen, auf wieviel Zinsen man zumindest theoretisch per 14. Juni des Folgejahres Anspruch hat, dann ist zu
berücksichtigen, dass die Bank nun auch Zinsen auf die Zinsen zahlt, die sie zum letzten Jahresultimo gutgebracht hat. Das Thema
Zinseszinsen folgt im nächsten Kapitel.
Zusammenfassung
Wir haben unter Anwendung der im Kapitel "Prozentrechnung" favorisierten Schreibweise einfache Zinsrechnungen durchgeführt. Hierbei haben wir die Begriffe Bar- und Gegenwartswert einerseits sowie End- und Zukunftswert andererseits kennen gelernt. Zukunftswerte wurden durch Aufzinsung ermittelt, Gegenwartswerte durch Abzinsung, wobei zunächst die jeweiligen Auf- bzw. Abzinsungsfaktoren ermittelt wurden.
Zinseszinsen
Dass die Zinsrechnung der mathematische Kern der Leasingkalkulation ist wurde eingangs schon gesagt. Bevor wir jedoch konkret auf Leasingkalkulation zu sprechen kommen, soll in diesem Kapitel noch ein wichtiger Grundstein zur Unterlegung des allgemeinen Verständnisses der Zinsrechnung gelegt werden.
Erweitern wir nun das Beispiel aus den vorhergehenden Kapiteln.
Wieder sei unser Ausgangszeitpunkt der 1. Januar. Nur diesmal beabsichtigst Du Dein Geld nicht ein sondern drei Jahre anzulegen. Der Zinssatz soll wieder 2% pro Jahr sein. Die Bank schreibt Dir jeweils zum Jahresende die bis dahin entstandenen Zinsen gut. Der Einzahlungsbetrag ist 1.500 €, sonstige Beträge werden und wurden nicht von Dir auf das Sparbuch eingezahlt. Weiterhin soll von nun ab auf die Angabe der Währung verzichtet werden. Gehen wir davon aus, dass es sich schlicht um Geldeinheiten handelt.
Klären wir zunächst schrittweise, was sich zum Anfang und Ende jedes Jahres auf Deinem Sparbuch befindet.
| Jahr | Barwert | Berechnung | Endwert |
|---|---|---|---|
| 1 | 1.500,00 | 1.500,00 * 1,02 | 1.530,00 |
| 2 | 1.530,00 | 1.530,00 * 1,02 | 1.560,60 |
| 3 | 1.560,60 | 1.560,60 * 1,02 | 1.591,81 |
Der jeweilige Barwert zum Jahresbeginn wird mit dem Aufzinsungsfaktor 1,02 multipliziert, um den Endwert des selben Jahres zu ermitteln. Das Ergebnis ist dann der Barwert zu Beginn des Folgejahres. Anders dargestellt ist der Endwert des Sparguthabens:

oder kurz
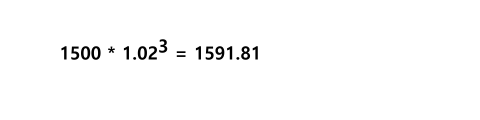
Wie zuvor wollen wir anhand dieses Beispiels uns ebenfalls anschauen, welcher Weg zur Berechnung des Barwerts führt, wenn nur der Endwert und der Zinssatz bekannt sind.
Auch hier heißt es, den Endwert mit dem inversen Aufzinsungsfaktor zu multiplizieren. Wie Du Dich erinnerst, ermittelt man den inversen Wert einer Zahl, indem man 1 durch sie teilt. Der entsprechende Abzinsungsfaktor ist also:
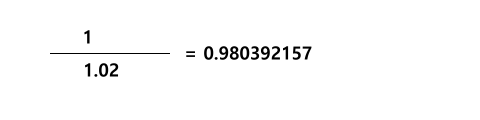
Also führt unser Weg zurück vom Endwert zum Barwert durch Berechnung von
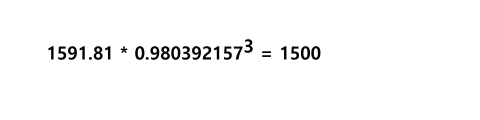
An dieser Stelle soll die erste allgemeine Regel verfasst werden:
Es gilt:
BW = Barwert
ZW = Zukunftswert
ZZR = Anzahl der Zahlungsperioden
F = Aufzinsungsfaktor
f = Abzinsungsfaktor
i = Zinssatz pro Periode
Dann lautet die Formel zur Berechnung des Zukunftswertes einer Einzahlung, die in aufeinander folgenden gleich langen Perioden zu einem gleich hohen Zinssatz verzinst wird:
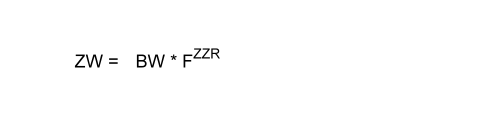
Wobei gilt: F = 1 + i
Die Formel zur Berechnung des Barwertes eines Zukunftswerts bei zurückliegenden aufeinander folgenden gleich langen Perioden und jeweils gleichem Zinssatz pro Periode lautet:
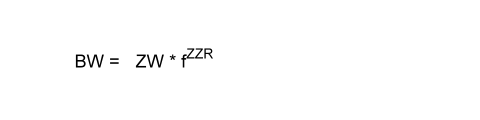
Wobei gilt: f = 1/F
Barwert einer Leasingrate
Die Bedeutung von Barwert und Endwert haben wir in dem vorangegangenen Kapitel geklärt. Ein Geldbetrag mit einem zu einem Stichtag bekannten Wert wächst bei gegebener Verzinsung über eine bestimmte Zeit bis schließlich der Zukunfstwert erreicht ist. Umgekehrt kann man bei bekannter Verzinsung von einem bekannten zukünftigen Wert auf den Barwert zu einem zeitlich vorgelagerten Stichtag schließen.
Barwert einer nachschüssigen Leasingrate
Als nächstes wollen wir den Barwert einzelner Leasingraten berechnen. Hierzu folgende Ausgangswerte:
Leasingnehmer und Leasinggesellschaft vereinbaren die Nutzungsüberlassung eines Computers auf drei Jahre, also 36 Monate. Der Anschaffungswert des Computers ist 5.000, die 36 mal zum jeweiligen Monatsende zu zahlende Leasingrate beträgt 154,39, die Leasinggesellschaft erzielt 7% p. a. (p. a. = per annum = pro Jahr) durch die zu zahlenden Leasingraten. Es handelt sich um einen Vollamortisationsleasingvertrag. Kurz notiert ist folgendes festzuhalten:
| Vertragstyp | Vollamortisation |
| Anschaffungswert (BW) | 5.000 |
| Anzahl Perioden (ZZR) | 36 |
| Leasingrate (RMZ) | 154,39 |
| Zins p. a. | 7% |
| Zahlungsfälligkeit | monatlich nachschüssig |
Hier treten wieder einige neue Aspekte der Finanzmathematik auf. Für weiterführende Aufgaben ist es sinnvoll, sich bewusst zu machen, dass der Anschaffungswert für die Leasinggesellschaft eine Auszahlung darstellt, die zu einem bestimmten Zeitpunkt getätigt wird. Obwohl es selten der Realität entspricht, gehen die meisten Leasinggesellschaften innerhalb ihrer Kalkulation davon aus, dass die Auszahlung des Anschaffungswertes und der Beginn der Überlassung des Leasingobjekts zum selben Zeitpunkt geschehen. Die Leasingraten als Entgelt für die Nutzungsüberlassung stellen Einzahlungen dar. Somit ist der Kalkulationszeitraum in aller Regel bestimmt durch Beginn und Ende der Nutzungsüberlassung.
Zinssätze werden üblicherweise als Zins pro Jahr ausgedrückt. Was in den bisherigen Ausführungen einfach gegeben war, müssen wir uns ab jetzt besonders bewusst machen. Der im Beispiel genannte Zinssatz stellt einen Jahreszinssatz dar.
Die Leasingraten fallen monatlich in gleicher Höhe an. Man spricht in diesem Zusammenhang von einer Annuität. Weiterhin sind die Leasingraten nachschüssig fällig, also zum Ende jeder Periode bzw. zum Ende jedes Monats während der Gebrauchsüberlassung. Auch dies ist ein Aspekt, der dem Leser klar sein muß.
Bevor wir uns jetzt der eigentlichen Aufgabenstellung zuwenden, sollen die o. g. Aspekte noch mal deutlich gelistet werden:
1)
Die Zahlung des Anschaffungswertes ist eine Auszahlung der Leasinggesellschaft.
2)
Die zu zahlenden Leasingraten stellen für die Leasinggesellschaft Einzahlungen dar.
3)
Der Kalkulationszeitraum beginnt mit dem Beginn der Nutzungsüberlassung und endet mit dem Ende der Nutzungsüberlassung. Dies ist zumindest der Regelfall. Bei komplexeren Leasingengagements kann der Kalkulationszeitraum auch vom Nutzungszeitraum abweichen.
4)
Zinssätze werden für gewöhnlich als Jahreszinsätze angegeben. Dies muß man berücksichtigen, wenn man z. B. mit monatlichen Raten kalkuliert.
5)
Leasingraten können vor- oder nachschüssig (selten auch mittelschüssig) fällig werden. Sind z. B. monatliche Raten vereinbart, heißt vorschüssig, dass die Leasingrate zu Beginn jedes Nutzungsmonats gezahlt wird, wohingegen nachschüssige Leasingraten zum Ende jedes Nutzungsmonats gezahlt werden. Dies wirkt sich auf die Kalkulation aus.
Zur Verallgemeinerung spricht man häufig nicht von konkreten Zeitdaten. Der Buchstabe "t" (t für tempus = Zeit (Latein) oder auch das englische time ) dient oft als Platzhalter für eine Periode, also zum Beispiel einen Monat. t1 z. B. ist der erste Monat, t2 der zweite Monat usw. Wer solche Verallgemeinerungen nicht mag, kann sich ja statt des "t" tatsächliche Daten ausdenken und z. B. für t1 den Januar eines Jahres nehmen. Die Verwendung des Buchstaben t für Zeitpunkte und -räume entspricht den Konventionen der Mathematiker. t0 wird gemäß diesen Konventionen häufig als Bezeichner für den Beginn des Betrachtungszeitraums gewählt.
Es gibt also 36 Leasingraten, die jeweils zum Ende (nachschüssig) von t1 bis t36 gezahlt werden. Betrachten wir nun eine beliebige Leasingrate etwas genauer. Wie ermitteln wir beipielsweise den Barwert der Leasingrate in t12 zu Beginn des Kalkulationszeitraums, also in t0. Hierzu nehmen wir die erste allgemeine Regel aus dem Kapitel "Zinseszinsen", nämlich

Wobei gilt: f = 1/F und F = 1 + i
Doch Vorsicht, unser "i" ist diesmal nicht der Jahreszinssatz. Da wir hier in Monatsperioden rechnen, ist i nur der auf den Monat entfallende Teil des Jahreszinssatzes. Wir müssen also den Jahreszinssatz durch 12 teilen, so dass sich ergibt
i = 7%/12 => d. h. 7/100/12 => d. h. 7/1200 = 0,0058333
Also ist F = 1 + 0,0058333 = 1,0058333 und f = 1/F also 1/1,0058333 = 0,99420053
Demzufolge ist der Barwert der 12. Rate zu Beginn des Betrachtungszeitraums t0:

Der eine oder andere mag es schon ahnen. Führt man diese Abzinsung für jede einzelne Leasingrate durch, so erhält man 36 auf t0 bezogene Barwerte, deren Summe 5.000 ist (vgl. Anschaffungswert des Computers). Wie man sich den allerdings immensen Rechenaufwand erspart, der durch die Berechnung einzelner Barwerte entsteht, wird in den folgenden Kapiteln behandelt.
Barwert einer vorschüssigen Leasingrate
Noch einmal zur Wiederholung. Vorschüssig bedeutet fällig zum Anfang der jeweiligen Periode. Das bedeutet zum Beispiel für die erste Leasingrate, dass sie am Anfang von t1 (bei nachschüssig wäre es das Ende von t1) gezahlt wird.
Die Ausgangsdaten für das vorschüssige Beispiel sind:
| Vertragstyp | Vollamortisation |
| Anschaffungswert (BW) | 5.000 |
| Anzahl Perioden (ZZR) | 36 |
| Leasingrate (RMZ) | 153,49 (nicht verwechseln, oben 154,39) |
| Zins p. a. | 7% |
| Zahlungsfälligkeit | monatlich vorschüssig |
Eine kleine Übungsfrage:
Wie lautet der Barwert der ersten Leasingrate in t0 ?
Antwort:
Der Barwert der ersten (wohlbemerkt vorschüssigen) Leasingrate ist die Rate selbst (im Beipiel also 153,49), da wir auf den Beginn von t1 (entspricht t0) abzinsen müssen
und die erste Rate auch zu Beginn von t1 fällig ist. Demzufolge zinsen wir über null Monate ab.
In diesem Frage-Antwort-Spiel liegt auch schon der Kern der vorschüssigen Zahlungsweise. Während wir bei der nachschüssigen Zahlungsweise die erste Rate bereits über einen Monat abzinsen müssen, muß die erste Rate bei vorschüssiger Zahlungsweise nicht abgezinst werden. Dies setzt sich für alle folgenden Raten fort. Die zweite Rate wird nachschüssig über zwei Perioden abgezinst und vorschüssig nur über eine Periode. Das heißt, dass in der hier angewandten finanzmathematischen Theorie das Ende der einen Periode gleichzeitig der Anfang der direkt folgenden Periode ist.
Wie lautet dann zum Beispiel der Barwert der vorschüssigen Leasingrate in t5 in t0 ?
Im Prinzip können wir dieselbe allgemeine Formel verwenden wie oben. Jedoch müssen wir berücksichtigen, dass unser ZZR nicht 5 sondern 5 - 1 = 4 (allgemein: ZZR-1) ist, so dass die allgemeine Formel zur Berechung des Barwerts einer vorschüssigen Leasingrate lautet:
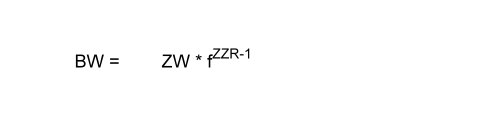
Übertragen wir die Beispieldaten auf die Formel so lautet der Barwert der Leasingrate aus t5 in t0

Selbstverständlich gilt auch hier, dass die Summe der Barwerte aller vorschüssigen Leasingraten in t0 5.000 ergibt.
Mittelschüssige Leasingraten
Mittelschüssige Leasingratenzahlung wird nur selten vereinbart. Möglicherweise liegt das daran, dass den verhandelnden Parteien, also Leasinggesellschaft und Leasinginteressent, der Sinn der mittelschüssigen Zahlung nicht ganz einleuchten will. Das Thema "Barwert einer mittelschüssigen Leasingrate" wird an dieser Stelle ausgelassen, da Mittelschüssigkeit erstens nur selten vorkommt und zweitens im aktuellen Gedankengang nur Verwirrung stiften würde.
Vor einem Irrtum soll der Leser jedoch bewahrt werden. Mittelschüssig heißt nicht unbedingt fällig zur Mitte des Kalendermonats, sondern fällig zur Mitte der Rechenperiode. Diesem Irrtum erliegen bisweilen sogar gestandene Leasingfachkräfte. Beginnt die Nutzungsüberlassung des Leasingobjekts
z. B. zum 15.04. , dann ist die erste monatlich und mittelschüssig fällige Leasingrate zum 01.05. fällig.
Zusammenfassung
In diesem Kapitel haben wir den Barwert einzelner Leasingraten zum Beginn des Kalkulationszeitraumes ermittelt. Hierbei mussten wir insbesondere zwischen Jahreszinsen und Monatszinsen zu unterscheiden lernen. Ferner haben wir die Begriffe vorschüssig und nachschüssig genauer kennen gelernt und die mit diesen Begriffen zusammenhängenden finanzmathematischen Besonderheiten erörtert.
Barwert eines Zahlungsstroms
Im vorherigen Kapitel haben wir den Barwert einer beliebigen Leasingrate errechnet. Nun wollen wir uns eine Methode erarbeiten, den Gegenwartswert mehrerer Leasingraten auf einmal zu berechnen. Folgen mehrere Zahlungen aufeinander, was typisch ist für Leasingratenzahlungen, spricht man von einem Zahlungsstrom.
Wer sich bisher fragt, warum denn der Barwert so wichtig ist, dem seien zwei Hinweise gegeben. Zum einen spielt er bei vielen Fachdisziplinen eine entscheidende Rolle. Zu nennen wären hier unter anderem nationale und internationale Rechnungslegungserfordernisse, Controlling und auch die im Geschäftsverkehr mit Banken betriebene so genannte Forfaitierung. Zum anderen, für das in diesem Beitrag behandelte Thema, bietet die Barwertformel eine gute Ausgangsbasis, um auf die Berechnung weiterer Werte innerhalb der Leasingkalkulation zu schließen. Deshalb wird die Barwertermittlung allen anderen Themen wie z. B. Berechnung einer Leasingrate oder Berechnung der Leasingvertragsdauer vorangestellt.
Barwert eines Zahlungsstroms bei nachschüssiger Zahlungsweise
Schaffen wir uns zunächst wieder Beispieldaten:
| Vertragstyp | Vollamortisation |
| Anschaffungswert (BW) | 4.422,11 |
| Anzahl Perioden (ZZR) | 24 |
| Leasingrate (RMZ) | 200,00 |
| Zins p. a. | 8% |
| Zahlungsfälligkeit | monatlich nachschüssig |
Der Barwert einer einzelnen nachschüssigen Leasingrate wird mit der nachstehenden Formel ermittelt, wobei hier das ZZR die für die einzelne Rate anzuwendende Periode ist
also für die erste Rate = 1, die zweite Rate = 2 usw.:

Beginnen wir mit der Bestimmung des Abzinsungsfaktors. Hierbei ist wieder zu beachten, dass die 8% Jahreszins in einem Monatszins umzurechnen sind.
Also ist unser Abzinsungsfaktor
i = 8 / 100 /12 = 8 / 1200 = 0,006667
F = 1 + i = 1,006667
f = 1 / F = 0,993377
in einem geschrieben
f = 1 / (1 + (8 / 1200)) = 0,993377
Um den Barwert des gesamten Zahlungsstroms (im Beispiel die 24 Leasingraten je 200) zu berechnen, könnte man die einzelnen Barwerte der Leasingraten addieren, so dass sich ergibt:

Um zu einer platzsparenderen Formel zu gelangen, bedienen sich Mathematiker folgender Methode.
Zuerst schafft man sich eine weitere Gleichung, indem man die erste Gleichung nochmal notiert, wobei man jedoch jeden Wert der Gleichung mit dem Abzinsungsfaktor multipliziert. Diese zweite Formel sieht dann folgendermaßen aus:

Auf der rechten Seite der Gleichung ist zu beobachten, dass sich der Exponent jeweils um 1 erhöht hat, so dass das z. B. das letzte Glied jetzt statt mit 24 mit 25 potenziert wird.
In einem zweiten Schritt subtrahiert man nun die zweite Gleichung von der ersten, d. h. man subtrahiert die linke Seite der zweiten Gleichung von der linken Seite der ersten Gleichung und die rechte Seite der zweiten Gleichung von der rechten Seite der ersten Gleichung. So entsteht eine dritte Gleichung, die einerseits viel kürzer ist als die beiden Ausgangsgleichungen und andererseits immer noch den gesuchten Barwert enthält.
Zur Verdeutlichung des Subtraktionsverfahrens notieren wir beide Gleichungen noch einmal untereinander.


Was auf der jeweils rechten Seite der beiden Gleichungen zu erkennen ist, ist, dass beide Gleichungen übereinstimmende Glieder haben. Streicht man diese Glieder aus, d. h. subtrahiert man sie voneinander, so bleibt letztlich nur noch folgendes über:
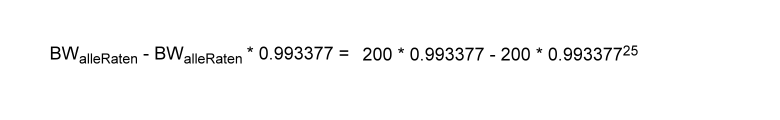
Da die gesuchte Größe jedoch der Barwert des Zahlungsstrom ist muß diese Gleichung erst noch ein wenig umgeschrieben werden und dann nach dem gesuchten Barwert aufgelöst werden. Die Umschreibung gestaltet sich folgendermaßen:

Diese Umschreibung mag auf den ersten Blick nicht gleich nachvollziehbar sein. Geht man jedoch her und multipliziert auf der rechten Seite den Wert BWalleRaten mit jedem Wert in der Klammer, so erhält man den vorherigen Ausdruck. Das gleiche kann man mit der linken Seite machen, indem man 200*0,993377 einerseits mit 1 multipliziert und anderseits mit -0,993377. Auch hier gelangt man dann wieder zur vorhergehenden Form der Gleichung.
Nun gilt es nur noch, die Gleichung nach BWalleRaten umzustellen, indem man beidseitig durch (1-0,993377) dividiert. Das Ergebnis lautet dann:

Die allgemeine Gleichung zur Berechnung des Barwerts eines nachschüssigen Leasingratenstroms lautet dann:

wobei gilt: f = 1 / F und F = 1 + i
Barwert eines Zahlungsstroms bei vorschüssiger Zahlungsweise
Als nächstes wollen wir untersuchen, was zu beachten ist, wenn statt nachschüssiger eine vorschüssige Zahlungsweise vereinbart ist. Es empfiehlt sich, dass man in diesem Zusammenhang noch einmal kurz einen Blick auf die Berechnung des Barwerts einer vorschüssigen Leasingrate aus dem Vorkapitel wirft. Die Methode zur Herleitung der entsprechenden Formel soll analog zur oben angewandten Methode erfolgen. Notieren wir uns also zunächst die Addition der einzelnen Barwerte unter Verwendung der allgemeinen Platzhalter.
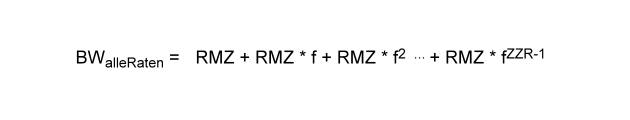
Jetzt bilden wir genau wie oben die zweite Gleichung, indem wir auf beiden Seiten mit f multiplizieren.
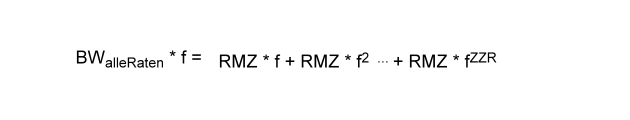
Wie zuvor ergibt sich, dass das letzte Glied der Gleichung einmal mehr potenziert wird als das letzte Glied der ersten Gleichung. Subtrahiert man nun wieder die sich entsprechenden Seiten der zweiten Gleichung von denen der ersten Gleichung so ergibt sich

Die so entstandene Gleichung lösen wir nach BWalleRaten in zwei Schritten auf und erhalten die allgemeine Gleichung zur Berechnung des Barwerts eines vorschüssigen Leasingratenstroms
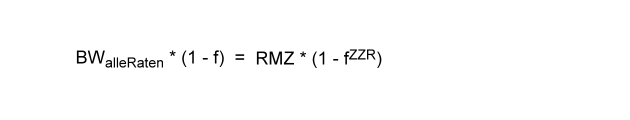
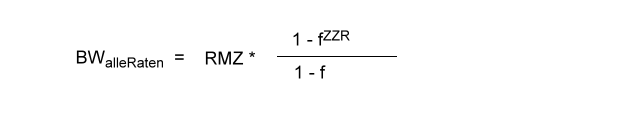
wobei gilt: f = 1 / F und F = 1 + i
Zusammenfassung
Nachdem wir im vorherigen Kapitel den Barwert einzelner Leasingraten berechnet haben, haben wir in diesem Kapitel gelernt, wie man den Barwert mehrerer aufeinanderfolgender Leasingraten auf einmal berechnet. Hierbei ist zu beachten, dass Voraussetzung für die Gültigkeit der allgemeinen Gleichungen ist, dass die Leasingraten jeweils gleich hoch sind und in gleichen Abständen gezahlt werden. Diese Voraussetzungen sind allerdings in der Praxis fast immer erfüllt. Ferner haben wir festgestellt, dass die Zahlungsperioden (z. B. monatlich, vierteljährlich, halbjährlich) in der jeweiligen Berechnung beachtet werden müssen, indem man den Zins pro Periode korrekt erfasst und die Anzahl der Perioden der Anzahl der Zahlungen anpasst.
Barwert von Leasingraten und Restwert
In der kaufmännischen Betrachtung ist der Restwert, der Wert, den der Leasinggeber zum Ende des Leasingengagements voraussichtlich über die periodischen Zahlungen des Leasingnehmers hinaus erzielt. In der Regel ist es so, dass der Restwert der Teil der Anschaffungskosten des Leasingobjekts ist, der nicht durch die periodischen Zahlungen des Leasingnehmers getilgt wird. Gleichwohl berechnet der Leasinggeber dem Leasingnehmer die Zinsen, die bis zum Ablauf des Leasingvertrags auf den Restwert entfallen. Der Restwert ist zudem eine kalkulatorische und oftmals geschätzte Größe, die für die Kalkulation der periodischen Zahlungen angenommen wird. Wie und in welcher tatsächlichen Höhe der Leasinggeber den Restwert realisiert, hängt von verschiedenen Faktoren ab, die ich hier nicht weiter vertiefe. In Deutschland finden sich in der Leasingratenkalkulation berücksichtigte Restwerte meistens in sogenannten Teilamortisationsverträgen. Im anglo-amerikanischem Raum spricht man von Non-Full-Payout Contracts, wobei hier der Name, wie so oft im Englischen, in einfacher Weise selbstsprechend ist.
Die Berechnung des Barwerts von Leasingraten und Restwert ist insofern einfach für alle, die bis zu diesen Abschnitt alles gelesen und verstanden haben, als dass wir nur Teile zusammenführen müssen, die in den Vorkapiteln behandelt wurden. Wir nehmen zum einen die Berechnungsformel zur Berechnung eines Leasingratenstroms und bezogen auf den Restwert die Formel zur Berechnung des Barwerts einer Leasingrate.
Barwert eines Leasingratenstroms + Barwert des Restwerts = Gesamtbarwert (Barwert des Leasingvertrags)
Barwert des Leasingvertrages bei nachschüssiger Zahlungsweise und Restwert

Barwert des Leasingvertrages bei vorschüssiger Zahlungsweise und Restwert

wobei gilt: f = 1 / F und F = 1 + i
Der den Restwert betreffende Teil der zwei Formeln ist gleich, weil in beiden Fällen die Fälligleit zum Vertragsende unterstellt wird.
Vollamortisationsleasingrate
Berechnung von nachschüssigen Vollamortisationsleasingraten
In den bisherigen Kapiteln haben wir uns Funktionsgleichungen erarbeitet, die die Abhängigkeit der Größe Barwert von den Größen Laufzeit, Leasingrate, Zins und gegebenenfalls Restwert darstellen. Hierbei haben wir uns genauere Gedanken über das Wesen von nach- bzw. vorschüssigen Fälligkeiten, zahlungsintervallbezogenen Zinssätzen und der Anzahl von Zahlungen innerhalb des gesamten Kalkulationszeitraums gemacht. Diese Überlegungen waren (hoffentlich) in nachvollziehbarer Weise, also mit geringem Abstraktionsgrad, an der reellen Praxis angelehnt. Beispielhaft hierfür soll noch einmal die Erkenntnis genannt werden, dass vorschüssige Leasingraten im Vergleich zu nachschüssigen Leasingraten der gleichen Periode, um eine Periode weniger abgezinst werden müssen, um ihren Barwert zu einem bestimmten Zeitpunkt zu erhalten. Diesen arbeitsintensiven aber heffentlich auch für den Einsteiger erhellenden Pfad wollen wir nun verlassen und mit den Mitteln der Gleichungslehre weitere Erkenntnisse sammeln.
Die Funktionsgleichung zur Berechnung des Barwerts enthält auch die gesuchte Größe dieses Kapitels, nämlich die Leasingrate. Es bietet sich an, die Gleichung nach dem Wert RMZ (Leasingrate) aufzulösen, um somit relativ schnell unsere Gleichungssammlung zu erweitern. In der nachstehenden Tabelle steht jeweils links die Gleichung bzw. das Umformungsergebnis und rechts der jeweilige Umformungsschritt. Ausgangspunkt ist die Gleichung zur Berechnung des Barwerts eines nachschüssigen Leasingratenstroms.
| Gleichung | Umformungsschritt |
|---|---|
 |  |
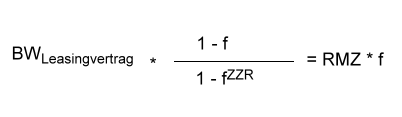 | 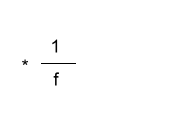 |
 | Durch das zusätzliche Umdrehen der Seitenliest sich die Gleichung intuitiver. |
Berechnung von vorschüssigen Vollamortisationsleasingraten
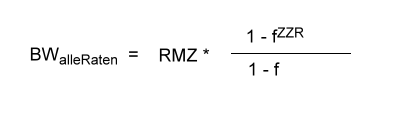
Bei der Umstellung der Gleichung zur Berechnung des Barwerts eines vorschüssigen Leasingratenstroms fasse ich mich etwas kürzer.
| Gleichung | Umformungsschritt |
|---|---|
 | entsprechend |
 |
wie üblich gilt: f = 1 / F und F = 1 + i
Vielleicht fragst Du Dich, was denn für BWLeasingvertrag einzusetzen ist. Das ist die Auszahlung des Leasinggebers zu Beginn. Also in der Regel der Anschaffungswert des Leasingobjekts. Die anfängliche Auszahlung des Leasinggebers kann aber beeinflusst werden von z. B. Provisionen an Dritte, Subventionen etc.
Teilamortisationsleasingraten
Wir können es uns recht einfach machen, wenn es um die Berechnung der Leasingrate geht, wenn ein Restwert zu berücksichtigen ist. Der entscheidende Punkt ist hierbei, dass der Restwert nicht getilgt aber verzinst wird, und das Periode für Periode (Monat, Quartal etc.) Wir können die Berechnung daher folgendermaßen aufteilen:
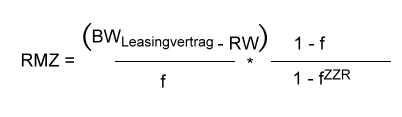
Berechnung von nachschüssigen Teilamortisationsleasingraten
Auf Basis der Berechnungsformel für nachschüssige Vollamortisationsleasingraten
| zu tilgender Teil | Restwert |
|---|---|
 |  |
Berechnung von vorschüssigen Teilamortisationsleasingraten
Auf Basis der Berechnungsformel für vorschüssige Vollamortisationsleasingraten
| zu tilgender Teil | Restwert |
|---|---|
 |  |
Erläuterung
Auf der jeweils linken Seite werden die Formeln aus dem Vorkapitel angewandt und zwar nur auf die anfängliche Auszahlung abzüglich des Restwerts =>
BWLeasingvertrag - RW.
Auf der rechten Seite addieren wir lediglich den periodischen Zins (z. B. monatlichen Zins hinzu). Die Besonderheit beim vorschüssigen Verfahren ist,
dass der periodische Zins nochmal mit seinem zugrundeliegenden Zinsatz abgezinst wird, da der Zins jeweils zu Beginn der Periode fällig wird.
Dies kann man "bequem" mit dem Abzinsungsfaktor machen.
Laufzeit berechnen
Will man die Laufzeit eines Leasingvertrags ermitteln, so kommt man mathematisch um einen gewissen Abstraktionsgrad nicht herum. Der Grund hierfür liegt darin, dass die Laufzeit bzw. die Anzahl der Zahlungsperioden durch eine Hochzahl repräsentiert wird, so dass der Kern der Übung die Auflösung einer Exponentialgleichung ist. Exponentialgleichungen löst man unter Zuhilfenahme des Logarithmus bzw. der Logarithmusgesetze auf. Somit empfiehlt sich zunächst ein Exkurs zum Thema Logarithmus, um dem anschließenden Lösungsweg zur Ermittlung der Laufzeit folgen zu können.
Logarithmus
Der Logarithmus stellt, wie schon gesagt, eine Hochzahl dar, also eine Zahl mit der man eine andere Zahl (Basis genannt) potenzieren muss, um eine angegebene Zahl zu erhalten. So ist z. B. der Logarithmus von 1000 zur Basis 10 die Zahl 3. D. h. 10 muß mit 3 potenziert werden, um 1000 zu erhalten. Die mathematische Schreibweise ist:
log10 1000 = 3
Leicht nachzuvollziehen ist sicherlich, dass 10 * 10 * 10 = 1000 sind. Schwieriger fällt das schon aus, wenn man die Aussage liest: log1,5 129,746338 = 12.
Bis zur Einführung des Taschenrechners hat man Logarithmen aus sog. Logarithmentafeln abgelesen, was mitunter ein mühseliges Unterfangen darstellte. Heute findet man auf jedem guten Taschenrechner Tasten für zwei "Standardlogarithmen", bei denen die Basis schon vorgeben ist. Es handelt sich einerseits um den Zehnerlogarithmus (Basis ist 10) und andererseits um den natürlichen Logarithmus (Basis ist die Eulersche Zahl e = 2,71828...). Für den Zehnerlogarithmus schreibt man statt log 10 b nur lg b und für den natürlichen Logarithmus statt log e b nur ln b. Zum rechnen mit Logarithmen hat die Mathematik Logarithmusgesetze entwickelt, von denen ein Gesetz hier aufgeführt werden soll, da es weiter unten zur Anwendung kommt.
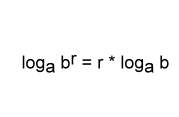
Dieses Logarithmusgesetz soll kurz durch ein einfaches Beispiel verdeutlicht werden:
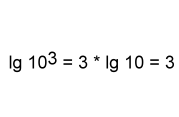
Der Zehnerlogarithmus von 103 (= 1000) ist 3, denn 10 hoch 3 ist 1000. 3 mal der Zehnerlogarithmus von 10 ist ebenfalls 3, denn lg 10 = 1 (101 = 10) und 3 * 1 ist 3.
Da die Ermittlung von Leasingvertragslaufzeiten unter Zuhilfenahme der Logarithmusgesetze bereits recht komplex ist, soll hier auf eine umfangreiche Darstellung mehrerer Varianten
zugunsten einer ausführlichen Erläuterung zur Ermittlung der Leasingvertragsdauer bei einem "nachschüssigen" Vollamortisationsleasingvertrag verzichtet werden.
Ausgangspunkt ist also:

Als ersten Schritt gilt es, die Funktionsgleichung so umzustellen, dass der Wert AnzahlPerioden möglichst separiert auf einer Seite der Gleichung steht.
| Gleichung | Umformungsschritt |
|---|---|
 |
 |
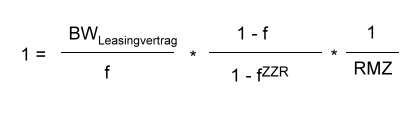 |
 |
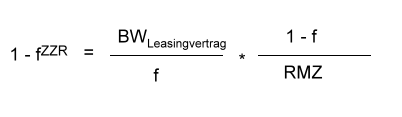 |
 |
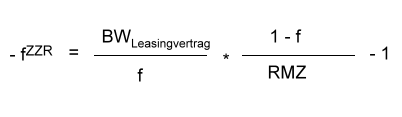 |
 |
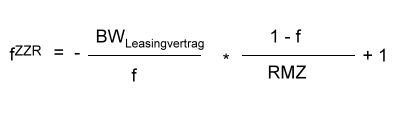 |
An dieser Stelle wollen wir die Umformung der Gleichung kurz unterbrechen und uns noch einmal den Sachverhalt mit dem oben genannten Logarithmusgesetz in Erinnerung rufen. Gesucht wird der Wert ZZR. Das oben erwähnte Logarithmusgesetz lautet: loga br = r * loga b. Setzen wir als nächstes den Zehnerlogarithmus in die Gleichung ein so steht links in der Gleichung lg fZZR, was dem Gesetz zur Folge gleich ZZR * lg f ist. Es geht also weiter mit
| Gleichung | Umformungsschritt |
|---|---|
 |
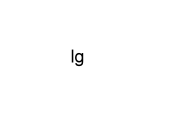 |
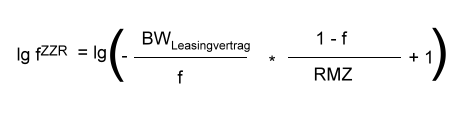 |
Anwendung des Logarithmusgesetzes auf der Linken Seite |
 |
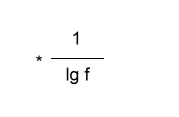 |
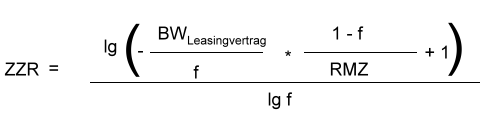 |
Ja, das ist schon etwas komplexer. Wer Lust hat, kann anhand folgender Werte mal nachvollziehen, welche Vertragslaufzeit bzw. Anzahl an Zahlungen sich bei diesen Beispieldaten errechnet. Setze in die obige letzte Gleichung ein:
| Vertragstyp | Vollamortisation |
| Anschaffungswert (BW) | 12.000 |
| Leasingrate (RMZ) | 376,04 (376,03639) |
| ZINS p. a. | 8% (f also 0,993377483) |
| Zahlungsfälligkeit | monatlich nachschüssig |
Wer hier 36 als Anzahl der Zahlungen (ZZR) errechnet, hat alles richtig gemacht.
Zins berechnen
Schaut man nach, wie MS Excel oder die in der Leasingbranche bekannten Taschenrechner der Firma Hewlett Packard (HP 12C, HP 17, HP 19B II) den Zins einer Zahlungsreihe berechnen, fällt auf, dass dabei keine Gleichung genutzt wird, in die man einfach die bekannten anderen Größen wie BW, ZZR, ZW etc. einsetzt, sondern von sog. Iterationen (Wiederholungen) gesprochen wird. Gemeint ist, dass man sich schrittweise an den gesuchten Wert - hier der Zins - herantastet. Dies im Wege der sogenannten Linearen Interpolation. Bei diesem Verfahren sucht man einen Funktionswert zwischen bekannten Funktionswerten einer nicht linearen Funktion, indem man von den Steigungen an den bekannten Punkten auf den Wert am gesuchten Punkt schliesst.
Zur Veranschaulichung schaffen wir zunächst wieder ein Rechenbeispiel:
| Vertragstyp | Teilamortisation |
| Anschaffungswert (BW) | 20.000 |
| Restwert (ZW) | 2.000 |
| Leasingrate (RMZ) | 1.681,62 |
| ZINS p. a. | 7% |
| ZZR | 12 |
| Zahlungsfälligkeit | vierteljährlich vorschüssig |
Da das Thema dieses Kapitels die Zinsermittlung ist, gehen wir davon aus, dass wir den o. g. Zinssatz von 7% gar nicht kennen.
Machen wir zum Einstieg nun einige Beobachtungen. Wir schauen uns zunächst an, welche Barwerte (Anschaffungswerte) wir errechnen, wenn wir in die allgemeine Gleichung "Barwert des Leasingvertrags bei vorschüssiger Zahlungsweise und Restwert" die Zinssätze 2%, 3%, 4% und 5% einsetzen.

| ZINS p. a. | Barwert (BW) | Veränderung des Barwerts |
|---|---|---|
| 2% | 21.520,13 | |
| 3% | 21.201,87 | 318,26 |
| 4% | 20.890,92 | 310,95 |
| 5% | 20.587,10 | 303,82 |
Generell zu beobachten ist, dass sich mit Erhöhung des Zinssatzes der Barwert vermindert. Ebenso vermindert sich die jeweilige Veränderung des Barwerts. Die hier wesentliche Beobachtung ist jedoch, dass bei gleichgroßen Zinssprüngen keine gleichgroßen Barwertveränderungen entstehen. Das heißt, das Verhältnis zwischen Zins und Barwert ist nicht linear. Umgekehrt kann man von fast linear sprechen, wie die unten abgebildete Kurve, die fast wie eine Gerade aussieht, verdeutlicht.
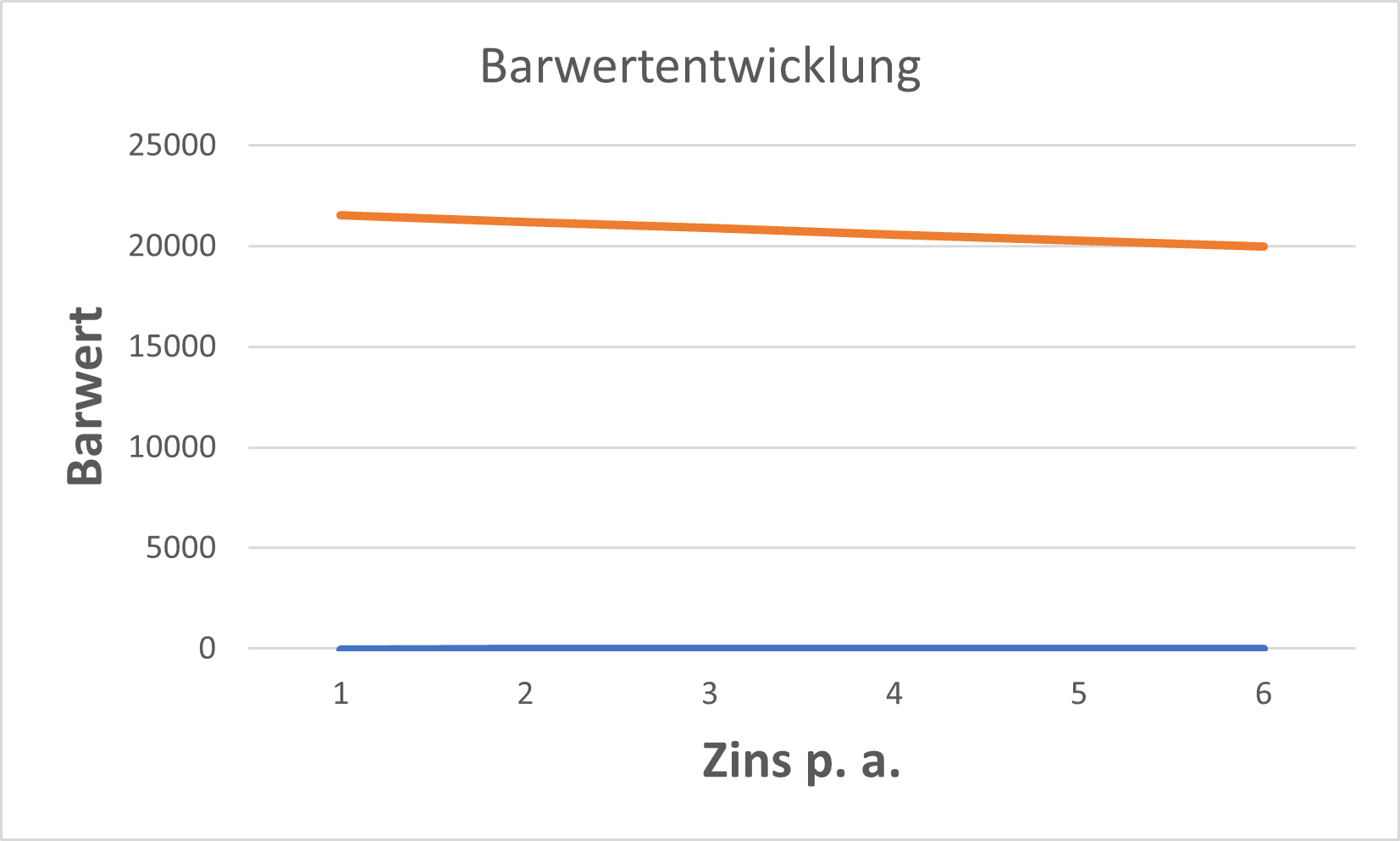
Dieser generelle Kurvenverlauf ist typisch für Zahlungsströme aus Leasingengagements. Schauen wir uns nun an, wie wir uns an den gesuchten Zins "herantasten". Hierzu habe ich in MS Excel eine Tabelle erstellt, die das iterative Verfahren darstellt:
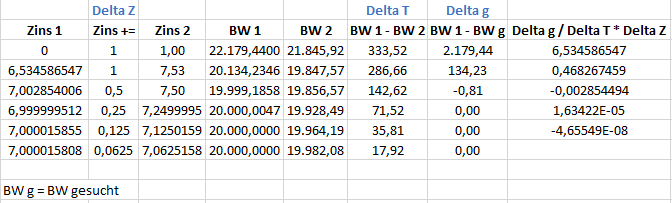
Ich bitte die kleine Darstellung zu entschuldigen. Um die Darstellungen möglichst auch auf mobilen Endgeräten zu ermöglichen, musste ich die Bildgröße limitieren.
So, was geschieht nun in der Tabelle. Mal in hoffentlich einfachen Worten beschrieben: Gesucht ist der Zinssatz, bei dessen Anwendung der Barwert des Leasingvertrags 20.000 entspricht.
Daher BW g (g = gesucht).
Beginnend mit einem Probezins 0 (Zins 1), einer Erhöhung um 1 (Delta Z) auf 1 (Zins 2), wird ermittelt welche Barwerte BW 1 und BW 2 entstehen. Aus der Differenz dieser beiden
Barwerte wird linear abgeleitet, wieviele Delta Z nötig sind, um BW g zu erreichen. Die übrigen Werte zur Barwertermittlung stammen aus dem Rechenbeispiel oben in diesem Kapitel.
Kennt man nun den Wert (in der Tabelle Delta g / Delta T * Delta Z), addiert man diesen zu dem zuvor genutzen Zins 1 hinzu und hat so einen neuen Probezins Zins 1. Ab hier beginnt
das "Spiel" von Neuem usw., wobei nach und nach die Erhöhung Delta Z verkleinert wird, um sich immer näher an BW g heran zu tasten.
Das Verfahren hat eine Abbruchbedingung, die vom Verfahrenden je nach Erfordernis zu bestimmen ist. Denkbar wäre das dann abgebrochen wird, wenn der Unterschied zwischen BW 1 und BW g
kleiner als 0,001 ist. Eine weitere eher aus Programmiersicht nötige Abbruchbedingung wäre, dass maximal 20 Iterationen durchlaufen werden, um zu vermeiden, dass bei "Konstruktionsfehlern"
eine sog. Endlosschleife entsteht.
Mittelschüssiges Rechnen
Wie im Kapitel "Barwert einer Leasingrate" erwähnt, kommt es nicht sehr häufig vor, dass in einem Leasingvertrag mittelschüssige Leasingratenzahlung vereinbart wird. Mir selbst ist die
mittlere Fälligkeit in vielen Jahren Leasingpraxis nur sehr, sehr selten begegnet. Damit der geneigte Leser jedoch auch bei diesem Thema mitreden kann, soll hier in aller Kürze auf
die Berechnung eines Barwerts eines mittelschüssigen Leasingratenstroms und auf die Ermittlung einer mittelschüssigen Leasingrate eingegangen werden.
Vorschüssige Leasingraten werden zu Beginn, nachschüssige am Ende der jeweiligen Periode fällig. Mittelschüssige Leasingraten werden, wie die Bezeichnung es schon ausdrückt, in der Mitte
der jeweiligen Periode fällig. Das heißt zum Beispiel bei vierteljährlicher Zahlungsweise und Mietbeginn zum 01. Januar des Jahres, dass die erste Leasingrate am 15. Februar fällig ist.
Die Herleitung der allgemeinen Gleichungen erfolgt analog zu den Verfahren, die im Kapitel "Barwert eines Zahlungsstroms" angewandt werden. Im Ergebnis sind die Barwertformeln für
nachschüssige Leasingraten und für mittelschüssige Leasingraten fast gleich. Der Unterschied besteht darin, dass die Leasingrate der ersten Periode nur zum halben Satz abgezinst wird.
Deswegen sind an dieser Stelle zwei neue Variablen einzuführen, die den Aufzinsungsfaktor (G) bzw. Abzinsungsfaktor (g) der jeweils ersten Periode darstellen.
G = 1 + (i / 2) und g = 1/G;
Sind G und g wie oben definiert dann lautet die Gleichung zur Berechnung des Barwerts eines mittelschüssigen Leasingratenstroms:
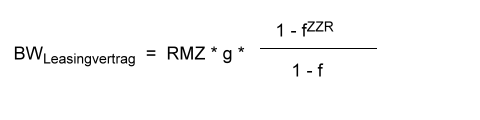
Demzufolge lautet dann die Gleichung zur Berechnung einer mittelschüssigen Leasingrate:

Zu den Definitionen von G und g treten natürlich auch die für F und f.
f = 1 / F und F = 1 + i
Wie immer finden die oben genannten Gleichungen Anwendung auf gleich hohe, in gleichen Zahlungsabständen zu zahlende Raten.
Degressive Leasingraten
Bei Leasingverträgen mit degressiven Leasingraten nehmen die Leasingraten im Verlauf der vereinbarten Leasingdauer ab. Beipielsweise könnten bei einem Vertrag über 24 Monate die ersten 12
Leasingraten 1.000 und die letzten 12 Leasingraten 800 betragen.
Die Frage, welche Formeln die Ausgangsbasis beim degressiven Rechnen sind, ist schnell beantwortet. Sie brauchen die, die einen Restwert berücksichtigen, selbst wenn es sich letztlich um
einen Vollamortisationsvertrag handelt. Viel interessanter ist jedoch, wie überhaupt "degressiv" gerechnet wird.
Dies läßt sich nur schrittweise realisieren. Nehmen wir an, der Anschaffungswert eines Leasingobjekts beträgt 10.000 und die vereinbarte Leasingdauer beträgt 36 Monate. Der Vertragstyp
ist Teilamortisationsvertrag. Es wird monatlich vorschüssig gezahlt. Der Jahreszinssatz ist 9,5%. Der Restwert nach drei Jahren beträgt 4.000, also 40% des Anschaffungswertes. Das heißt,
60% (6.000) des Anschaffungswertes werden durch die Zahlung der 36 Leasingraten amortisiert. Die Leasingratenhöhe vermindert sich jeweils nach einem Jahr.
Nun gilt es, den zu amortisierenden Teil des Anschaffungswertes, also 6.000, in drei Beträge zu zerlegen, die im Verhältnis zueinander abnehmend sind. Dies könnte zum Beispiel zu
folgender Aufteilung führen:
| 1. Jahr | 3.000 werden amortisiert |
| 2. Jahr | 2.000 werden amortisiert |
| 3. Jahr | 1.000 werden amortisiert |
Die Berechnung der jeweiligen Leasingraten erfolgt dann in drei Schritten unter Verwendung der Gleichung für die Berechnung einer vorschüssigen Teilamortisationsleasingrate
| zu tilgender Teil | Restwert |
|---|---|
 |  |
Einzusetzen für BWLeasingvertrag ist der zu Beginn der jeweiligen 12 Monate noch nicht amortisierte Teil des Investitionbetrages (im Beispiel der Anschaffungswert). Für RW ist der Teil einzusetzen, der nach Ablauf der jeweiligen 12 Monate noch nicht amortisiert ist. Für ZZR wird die Anzahl der Zahlungen eingesetzt, die in dem Zeitabschnitt gezahlt werden, für den die Leasingrate berechnet wird. ZZR beträgt also 12.
Berechnung der Leasingrate des 1. Jahres:
| zu tilgender Teil | Restwert |
|---|---|
 |  |
Zu Beginn der ersten 12 Monate sind 10.000 noch nicht amortisiert. 3.000 sollen amortisiert werden, also sind nach Ablauf der ersten 12 Monate noch 7.000 zu amortisieren.
Berechnung der Leasingrate des 2. Jahres:
| zu tilgender Teil | Restwert |
|---|---|
 |  |
Zu Beginn der zweiten 12 Monate sind 7.000 noch nicht amortisiert. 2.000 sollen amortisiert werden, also sind nach Ablauf der zweiten 12 Monate noch 5.000 zu amortisieren.
Berechnung der Leasingrate des 3. Jahres:
| zu tilgender Teil | Restwert |
|---|---|
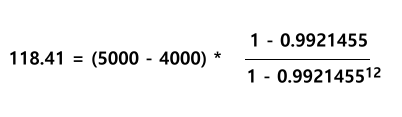 |  |
Zu Beginn der dritten 12 Monate sind 5.000 noch nicht amortisiert. 1.000 sollen amortisiert werden, also sind nach Ablauf der dritten 12 Monate noch 4.000 (Restwert) zu amortisieren.
Zusammenfassung
In diesem Kapitel wurde keine neue Gleichung eingeführt. Vielmehr ging es um die strukturierte Anwendung der bereits erarbeiteten Gleichungen zur Berechnung einer vor- bzw. nachschüssigen Teilamortisationsleasingrate, die auch Anwendung finden, wenn durch die Zahlung der Leasingraten voll amortisiert werden soll. Der Grund hierfür liegt darin, dass zum Ablauf des jeweiligen Zeitabschnitts der noch nicht amortisierte Teil des Investitionsbetrages rechnerisch wie ein Restwert behandelt wird.
| Begriff | Bedeutung |
|---|---|
| BW | Barwert |
| RMZ | periodische Zahlung (Regelmäßige Zahlung) |
| ZZR | Anzahl der periodischen Zahlungen |
| ZW, RW | Zukunfswert (Restwert) |
| i | Zinsatz pro Periode - z. B. 7% (p. a.) / 12 = 0,07 / 12 = 0,00583 |
| F | Aufzinszungsfaktor => 1 + i |
| f | Abzinszungsfaktor => 1 / F |